
So that Q = U - W, where U is the energy input to the system, and W is the part of that energy that goes into doing work. Some of that energy could easily be expressed as an amount of mechanical work done by the system (W, such as a hot gas pushing against a piston in a car engine). Suppose you pump energy, U, into a system, what happens? Part of the energy goes into the internal heat content, Q, making Q a positive quantity, but not all of it. This idea can lead us to an alternate form for equation 2, that will be useful later on. And, if the internal heat energy Q goes down (Q is a negative number), then the entropy will go down too.Ĭlausius and the others, especially Carnot, were much interested in the ability to convert mechanical work into heat energy, and vice versa. If Q is positive, then so is S, so if the internal heat energy goes up, while the temperature remains fixed, then the entropy S goes up. Here the symbol "" is a representation of a finite increment, so that S indicates a "change" or "increment" in S, as in S = S1 - S2, where S1 and S2 are the entropies of two different equilibrium states, and likewise Q. So, entropy in classical thermodynamics is defined only for systems which are in thermodynamic equilibrium.Īs long as the temperature is therefore a constant, it's a simple enough exercise to differentiate equation 1, and arrive at equation 2.
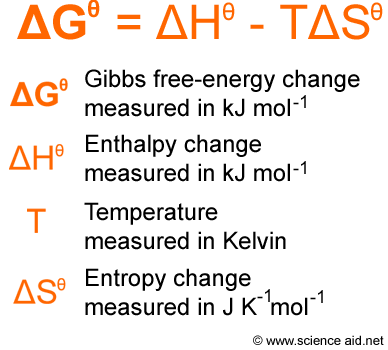
The temperature of the system is an explicit part of this classical definition of entropy, and a system can only have "a" temperature (as opposed to several simultaneous temperatures) if it is in thermodynamic equilibrium. Suffice for now to point out that what they called heat content, we would now more commonly call the internal heat energy. Later in the 19th century, the molecular theory became predominant, mostly due to Maxwell, Thomson and Ludwig Boltzmann, but we will cover that story later. It was Thomson who seems to have been the first to explicity recognize that this could not be the case, because it was inconsistent with the manner in which mechanical work could be converted into heat. Carnot & Clausius thought of heat as a kind of fluid, a conserved quantity that moved from one system to the other. At this time, the idea of a gas being made up of tiny molecules, and temperature representing their average kinetic energy, had not yet appeared. In equation 1, S is the entropy, Q is the heat content of the system, and T is the temperature of the system. The specific definition, which comes from Clausius, is as shown in equation 1 below. The concept was expanded upon by Maxwell (Theory of Heat, Longmans, Green & Co. But it was Clausius who first explicitly advanced the idea of entropy (On Different Forms of the Fundamental Equations of the Mechanical Theory of Heat, 1865 The Mechanical Theory of Heat, 1867). My goal here is to shwo how entropy works, in all of these cases, not as some fuzzy, ill-defined concept, but rather as a clearly defined, mathematical & physical quantity, with well understood applications.Ĭlassical thermodynamics developed during the 19th century, its primary architects being Sadi Carnot, Rudolph Clausius, Benoit Claperyon, James Clerk Maxwell, and William Thomson (Lord Kelvin). It did not take long for Claude Shannon to borrow the Boltzmann-Gibbs formulation of entropy, for use in his own work, inventing much of what we now call information theory. But the advent of statistical mechanics in the late 1800's created a new look for entropy.

There is no such thing as an "entropy", without an equation that defines it.Įntropy was born as a state variable in classical thermodynamics. Remember in your various travails, that entropy is what the equations define it to be. That means that entropy is not something that is fundamentally intuitive, but something that is fundamentally defined via an equation, via mathematics applied to physics. But it should be remembered that entropy, an idea born from classical thermodynamics, is a quantitative entity, and not a qualitative one. The popular literature is littered with articles, papers, books, and various & sundry other sources, filled to overflowing with prosaic explanations of entropy.


 0 kommentar(er)
0 kommentar(er)
